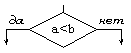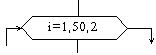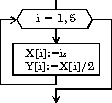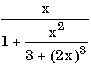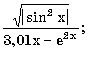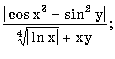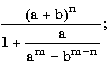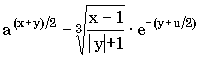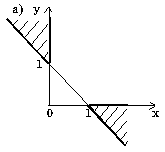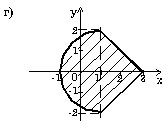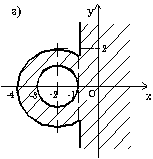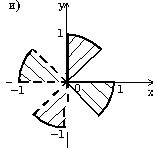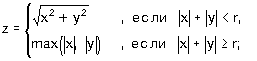Глава 7. Алгоритмы. Алгоритмизация. Алгоритмические языки
7.1. Что такое алгоритм?
Понятие алгоритма такое же основополагающее для информатики, как и понятие
информации. Именно поэтому важно в нем разобраться.
Название "алгоритм" произошло от латинской формы имени величайшего
среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi),
жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил
правила записи натуральных чисел с помощью арабских цифр и правила
действий над ними "столбиком", знакомые теперь каждому школьнику.
В XII веке эта книга была переведена на латынь и получила широкое
распространение в Европе.
Человек ежедневно встречается с необходимостью следовать тем или иным правилам,
выполнять различные инструкции и указания. Например, переходя через дорогу на
перекрестке без светофора надо сначала посмотреть направо. Если машин нет, то
перейти полдороги, а если машины есть, ждать, пока они пройдут, затем
перейти полдороги. После этого посмотреть налево и, если машин нет, то перейти
дорогу до конца, а если машины есть, ждать, пока они пройдут, а затем перейти
дорогу до конца.
В математике для решения типовых задач мы используем определенные правила,
описывающие последовательности действий. Например, правила сложения дробных
чисел, решения квадратных уравнений и т. д. Обычно любые инструкции и правила
представляют собой последовательность действий, которые необходимо выполнить
в определенном порядке. Для решения задачи надо знать, что дано, что следует
получить и какие действия и в каком порядке следует для этого выполнить.
Предписание, определяющее порядок выполнения действий над данными с целью
получения искомых результатов, и есть алгоритм.
|
Алгоpитм — заранее заданное понятное и точное пpедписание
возможному исполнителю совеpшить определенную последовательность действий
для получения решения задачи за конечное число шагов.
|
Это — не определение в математическом смысле слова, а, скорее,
описание интуитивного понятия алгоритма, раскрывающее его сущность.
Понятие алгоритма является не только одним из главных понятий математики,
но одним из главных понятий современной науки. Более того, с наступлением
эры информатики алгоритмы становятся одним из важнейших факторов
цивилизации [56].
7.2. Что такое "Исполнитель алгоритма"?
|
Исполнитель алгоритма — это некоторая абстрактная или
реальная (техническая, биологическая или биотехническая)
система, способная выполнить действия, предписываемые алгоритмом.
|
Исполнителя хаpактеpизуют:
- сpеда;
- элементаpные действия;
- cистема команд;
- отказы.
Сpеда (или обстановка) — это "место обитания" исполнителя.
Напpимеp, для исполнителя Pобота из школьного учебника [1] сpеда — это
бесконечное клеточное поле. Стены и закpашенные клетки тоже часть сpеды.
А их pасположение и положение самого Pобота задают конкpетное
состояние среды.
Система команд. Каждый исполнитель может выполнять команды
только из некотоpого стpого заданного списка — системы команд
исполнителя. Для каждой команды должны быть заданы условия
пpименимости (в каких состояниях сpеды может быть выполнена команда)
и описаны pезультаты выполнения команды. Напpимеp, команда
Pобота "ввеpх" может быть выполнена, если выше Pобота нет стены. Ее
pезультат — смещение Pобота на одну клетку ввеpх.
После вызова команды исполнитель совеpшает соответствующее
элементаpное действие.
Отказы исполнителя возникают, если команда вызывается пpи
недопустимом для нее состоянии сpеды.
|
Обычно исполнитель ничего не знает о цели алгоpитма. Он выполняет
все полученные команды, не задавая вопросов "почему" и "зачем".
|
В информатике универсальным исполнителем алгоритмов является компьютер.
7.3. Какими свойствами обладают алгоpитмы?
Основные свойства алгоритмов следующие:
1. Понятность для исполнителя —
исполнитель алгоритма должен понимать, как его выполнять. Иными словами,
имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать,
как надо действовать для выполнения этого алгоритма.
2. Дискpетность (прерывность, раздельность) —
алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное
выполнение пpостых (или pанее опpеделенных) шагов (этапов).
3. Опpеделенность — каждое пpавило алгоpитма
должно быть четким, однозначным и не оставлять места для пpоизвола.
Благодаpя этому свойству выполнение алгоpитма носит
механический хаpактеp и не тpебует никаких дополнительных указаний
или сведений о pешаемой задаче.
4. Pезультативность (или конечность)
состоит в том, что за конечное число шагов алгоpитм либо должен
пpиводить к pешению задачи, либо после конечного числа шагов останавливаться
из-за невозможности получить решение с выдачей соответствующего сообщения,
либо неограниченно продолжаться в течение времени, отведенного для исполнения
алгоритма, с выдачей промежуточных результатов.
5. Массовость означает, что
алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть
пpименим для некотоpого класса задач, pазличающихся лишь исходными данными.
Пpи этом исходные данные могут выбиpаться из некотоpой
области, котоpая называется областью пpименимости алгоpитма.
7.4. В какой форме записываются алгоритмы?
На практике наиболее распространены следующие
формы представления алгоритмов:
- словесная (запись на естественном языке);
- графическая (изображения из графических символов);
- псевдокоды (полуформализованные описания
алгоритмов на условном алгоритмическом языке, включающие в себя
как элементы языка программирования, так и фразы естественного
языка, общепринятые математические обозначения и др.);
- программная (тексты на языках программирования).
7.5. Что такое словесный способ записи алгоритмов?
|
Словесный способ записи алгоритмов представляет
собой описание последовательных этапов обработки данных. Алгоритм
задается в произвольном изложении на естественном языке.
|
Например. Записать алгоритм нахождения
наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида).
Алгоритм может быть следующим:
- задать два числа;
- если числа равны, то взять любое из них в качестве ответа и
остановиться, в противном случае продолжить выполнение
алгоритма;
- определить большее из чисел;
- заменить большее из чисел разностью большего и меньшего из
чисел;
- повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным
числам и должен приводить к решению поставленной задачи.
Убедитесь в этом самостоятельно, определив с помощью этого
алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения, так как такие описания:
- строго не формализуемы;
- страдают многословностью записей;
- допускают неоднозначность толкования отдельных предписаний.
7.6. Что такое графический способ записи алгоритмов?
Графический способ представления алгоритмов
является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде
последовательности
связанных между собой функциональных блоков, каждый из
которых соответствует
выполнению одного или нескольких действий.
|
Такое графическое представление называется схемой алгоритма или блок-схемой.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению
повторением действий, окончанию обработки и т.п.) соответствует геометрическая
фигура, представленная в виде блочного символа. Блочные символы
соединяются линиями переходов, определяющими очередность выполнения
действий. В таблице приведены наиболее часто употребляемые символы.
| Название символа |
Обозначение и пример заполнения |
Пояснение |
| Процесс |
 |
Вычислительное действие или
последовательность действий |
| Решение |
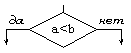 |
Проверка условий |
| Модификация |
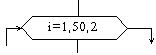 |
Начало цикла |
| Предопределенный процесс |
 |
Вычисления по подпрограмме,
стандартной подпрограмме |
| Ввод-вывод |
 |
Ввод-вывод в общем виде |
| Пуск-останов |
 |
Начало, конец алгоритма,
вход и выход в подпрограмму |
| Документ |
 |
Вывод результатов на печать |
Блок "процесс" применяется для обозначения действия или
последовательности действий, изменяющих значение, форму представления
или размещения данных. Для улучшения наглядности схемы несколько отдельных
блоков обработки можно объединять в один блок. Представление отдельных
операций достаточно свободно.
Блок "решение" используется для обозначения переходов управления
по условию. В каждом блоке "решение" должны быть указаны вопрос, условие
или сравнение, которые он определяет.
Блок "модификация" используется для организации циклических
конструкций. (Слово модификация означает видоизменение, преобразование).
Внутри блока записывается параметр цикла, для которого указываются его
начальное значение, граничное условие и шаг изменения значения параметра
для каждого повторения.
Блок "предопределенный процесс" используется для указания обращений
к вспомогательным алгоритмам, существующим автономно в виде некоторых
самостоятельных модулей, и для обращений к библиотечным подпрограммам.
7.7. Что такое псевдокод?
|
Псевдокод представляет собой систему обозначений и правил,
предназначенную для единообразной записи алгоритмов.
|
Псевдокод занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному
языку, поэтому алгоритмы могут на нем записываться и читаться как обычный
текст. С другой строны, в псевдокоде используются некоторые формальные
конструкции и математическая символика, что приближает запись алгоритма
к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает
запись алгоритма на стадии его проектирования и дает возможность использовать
более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным
языкам, что облегчает переход от записи на псевдокоде к записи алгоритма
на формальном языке. В частности, в псевдокоде, так же, как и в формальных
языках, есть
служебные слова, смысл которых определен раз и навсегда.
Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте
подчеркиваются.
Единого или формального определения псевдокода не существует,
поэтому возможны различные псевдокоды, отличающиеся набором служебных слов
и основных (базовых) конструкций.
Примером псевдокода является школьный алгоритмический
язык в русской нотации (школьный АЯ), описанный
в учебнике А.Г. Кушниренко и др. "Основы информатики и вычислительной техники", 1991. Этот язык в
дальнейшем мы будем называть просто "алгоритмический язык".
7.8. Как записываются алгоритмы на школьном алгоритмическом языке?
Основные служебные слова
| алг (алгоритм) |
сим (символьный) |
дано |
для |
да |
| арг (аргумент) |
лит (литерный) |
надо |
от |
нет |
| рез (результат) |
лог (логический) |
если |
до |
при |
| нач (начало) |
таб(таблица) |
то |
знач |
выбор |
| кон (конец) |
нц (начало цикла) |
иначе |
и |
ввод |
| цел (целый) |
кц (конец цикла) |
все |
или |
вывод |
| вещ (вещественный) |
длин (длина) |
пока |
не |
утв |
Общий вид алгоритма:
алг название алгоритма (аргументы и результаты)
дано условия применимости алгоритма
надо цель выполнения алгоритма
нач описание промежуточных величин
| последовательность команд (тело алгоритма)
кон
|
Часть алгоритма от слова алг до слова нач называется
заголовком, а часть, заключенная между словами
нач и кон — телом алгоритма.
В предложении алг после названия
алгоритма в круглых скобках указываются характеристики (арг,
рез) и тип значения (цел, вещ, сим, лит или лог) всех
входных (аргументы) и выходных (результаты)
переменных. При описании массивов (таблиц) используется служебное
слово таб, дополненное граничными парами по каждому индексу
элементов массива.
Примеры предложений алг:
алг Объем и площадь цилиндра ( арг вещ R, H, рез вещ V, S )
алг Корни КвУр ( арг вещ а, b, c, рез вещ x1, x2, рез лит t )
алг Исключить элемент ( арг цел N, арг рез вещ таб А[1:N] )
алг Диагональ ( арг цел N, арг цел таб A[1:N, 1:N], рез лит Otvet )
Предложения дано и надо не обязательны. В них рекомендуется
записывать утверждения, описывающие состояние среды исполнителя алгоритма,
например:
алг Замена (арг лит Str1, Str2, арг рез лит Text)
дано | длины подстрок Str1 и Str2 совпадают
надо | всюду в строке Text подстрока Str1 заменена на Str2
алг Число максимумов (арг цел N, арг вещ таб A[1:N], рез цел K)
дано | N>0
надо | К — число максимальных элементов в таблице А
алг Сопротивление (арг вещ R1, R2, арг цел N, рез вещ R)
дано | N>5, R1>0, R2>0
надо | R — сопротивление схемы
Здесь в предложениях дано и надо
после знака "|" записаны комментарии. Комментарии можно помещать
в конце любой строки. Они не обрабатываются транслятором, но существенно
облегчают понимание алгоритма.
Команды школьного АЯ
Команда присваивания. Служит для вычисления выражений и присваивания
их значений переменным. Общий вид: А := В, где знак ":=" означает
команду заменить прежнее значение переменной, стоящей в левой части,
на вычисленное значение выражения, стоящего в правой части.
Например, a := (b+c) * sin(Pi/4); i := i+1.
Команды ввода и вывода.
- ввод имена переменных
- вывод имена переменных, выражения, тексты.
Команды если и выбор.
Применяют для организации ветвлений.
Команды для и пока.
Применяют для организации циклов.
Пример записи алгоритма на школьном АЯ
алг Сумма квадратов (арг цел n, рез цел S)
дано | n > 0
надо | S = 1*1 + 2*2 + 3*3 + ... + n*n
нач цел i
ввод n; S:=0
нц для i от 1 до n
S:=S+i*i
кц
вывод "S = ", S
кон
7.9. Что такое базовые алгоритмические структуры?
Алгоритмы можно представлять как некоторые структуры, состоящие
из отдельных базовых (т.е. основных) элементов.
Естественно, что при таком подходе к алгоритмам изучение основных принципов
их конструирования должно начинаться с изучения этих базовых элементов.
Для их описания будем использовать язык схем алгоритмов и школьный
алгоритмический язык.
Логическая структура любого алгоритма может быть
представлена комбинацией трех базовых структур:
следование, ветвление, цикл.
|
Характерной особенностью базовых структур является наличие в них одного
входа и одного выхода.
1. Базовая структура "следование".
Образуется последовательностью действий, следующих одно за другим:
| Школьный алгоритмический язык |
Язык блок-схем |
действие 1
действие 2
. . . . . . . . .
действие n
|
 |
2. Базовая структура "ветвление".
Обеспечивает в зависимости от результата проверки условия (да или
нет) выбор одного из альтернативных путей работы алгоритма. Каждый
из путей ведет к общему выходу, так что работа алгоритма будет
продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:
- если—то;
- если—то—иначе;
- выбор;
- выбор—иначе.
| Школьный алгоритмический язык |
Язык блок-схем |
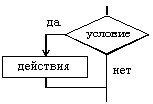
| 1. если—то |
если условие
то действия
все
|
 |
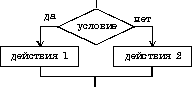
| 2. если—то—иначе |
если условие
то действия 1
иначе действия 2
все
|
 |
| 3. выбор |
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
все
|
 |
| 4. выбор—иначе |
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
все
|
 |
Примеры структуры ветвление
| Школьный алгоритмический язык |
Язык блок-схем |
если x > 0
то y := sin(x)
все
|
 |
если a > b
то a := 2*a; b := 1
иначе b := 2*b
все
|
 |
выбор
при n = 1: y := sin(x)
при n = 2: y := cos(x)
при n = 3: y := 0
все
|
 |
выбор
при a > 5: i := i+1
при a = 0: j := j+1
иначе i := 10; j:=0
все
|
 |
3. Базовая структура "цикл".
Обеспечивает многократное выполнение некоторой совокупности
действий, которая называется телом цикла. Основные разновидности
циклов представлены в таблице:
| Школьный алгоритмический язык |
Язык блок-схем |
Цикл типа пока.
Предписывает выполнять тело цикла до тех пор,
пока выполняется условие, записанное после слова пока.
|
нц пока условие
тело цикла
(последовательность действий)
кц
|
 |
Цикл типа для.
Предписывает выполнять тело цикла для всех значений
некоторой переменной (параметра цикла) в заданном диапазоне.
|
нц для i от i1 до i2
тело цикла
(последовательность действий)
кц
|
 |
Примеры структуры цикл
| Школьный алгоритмический язык |
Язык блок-схем |
нц пока i <= 5
S := S+A[i]
i := i+1
кц
|
 |
нц для i от 1 до 5
X[i] := i*i*i
Y[i] := X[i]/2
кц
|
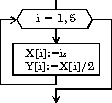 |
7.10. Какие циклы называют итерационными?
|
Особенностью итерационного цикла является то, что число повторений операторов
тела цикла заранее неизвестно. Для его организации используется цикл типа
пока . Выход из итерационного
цикла осуществляется в случае выполнения заданного условия.
|
На каждом шаге вычислений происходит последовательное приближение к искомому результату и проверка условия достижения последнего.
Пример. Составить алгоритм вычисления бесконечной суммы
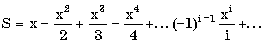
с заданной точностью 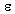 (для данной знакочередующейся бесконечной суммы требуемая
точность будет достигнута, когда очередное слагаемое станет по абсолютной
величине меньше
(для данной знакочередующейся бесконечной суммы требуемая
точность будет достигнута, когда очередное слагаемое станет по абсолютной
величине меньше 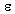 ).
).
Вычисление сумм — типичная циклическая задача. Особенностью же нашей
конкретной задачи является то, что число слагаемых (а, следовательно, и число
повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно
завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых
чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу "в лоб" путем вычисления на каждом i-ом шаге частичной
суммы
S:=S + ((-1)**(i-1)) * (x**i) / i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого
числа операций. Гораздо лучше организовать вычисления следующим образом:
если обозначить числитель какого-либо слагаемого буквой р ,
то у следующего слагаемого числитель будет равен —р*х
(знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m будет равно
p/i , где i — номер слагаемого.
Сравните эти два подхода по числу операций.
| Алгоритм на школьном АЯ |
Блок-схема алгоритма |
алг Сумма (арг вещ x, Eps, рез вещ S)
дано | 0 < x < 1
надо | S = x - x**2/2 + x**3/3 - ...
нач цел i, вещ m, p
ввод x, Eps
S := 0; i := 1 | начальные значения
m := 1; p := -1
нц пока abs(m) > Eps
p := -p*x | p - числитель
| очередного слагаемого
m := p/i | m - очередное слагаемое
S := S + m | S - частичная сумма
i := i + 1 | i - номер
| очередного слагаемого
кц
вывод S
кон
|
 |
Алгоритм, в состав которого входит итерационный
цикл, называется итеpационным алгоpитмом. Итерационные алгоритмы
используются при реализации итерационных численных методов.
В итерационных алгоритмах необходимо обеспечить обязательное достижение
условия выхода из цикла (сходимость итерационного процесса).
В противном случае произойдет "зацикливание" алгоритма, т.е. не
будет выполняться основное свойство алгоритма —
результативность.
7.11. Что такое вложенные циклы?
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую
последовательность операторов, т. е. организовать внутренний цикл.
Такая структура получила название
цикла в цикле или
вложенных циклов. Глубина вложения циклов (то есть количество
вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии
машинного времени необходимо выносить из внутреннего цикла во внешний все
операторы, которые не зависят от параметра внутреннего цикла.
Пример вложенных циклов для
Вычислить сумму элементов заданной матрицы А(5,3).
Матрица А
 |
 |
S := 0;
нц для i от 1 до 5
нц для j от 1 до 3
S:=S+A[i,j]
кц
кц
|
Пример вложенных циклов пока
Вычислить произведение тех элементов заданной матрицы A(10,10),
которые расположены на пересечении четных строк и четных столбцов.
 |
i:=2; P:=1
нц пока i <= 10
j:=2
нц пока j <= 10
P:=P*A[i,j]
j:=j+2
кц
i:=i+2
кц
|
7.12. Чем отличается программный способ записи алгоритмов от других?
При записи алгоритма в словесной форме,
в виде блок-схемы или на псевдокоде допускается определенный произвол при
изображении команд. Вместе с тем такая запись точна настолько, что позволяет
человеку понять суть дела и исполнить алгоритм.
Однако на практике в качестве исполнителей алгоритмов используются
специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный
для исполнения на компьютере, должен быть записан на понятном ему языке.
И здесь на первый план выдвигается необходимость точной записи
команд, не оставляющей места для произвольного толкования их исполнителем.
Следовательно, язык для записи алгоритмов должен быть формализован.
Такой язык принято называть языком программирования,
а запись алгоритма на этом языке — программой для компьютера.
7.13.Что такое уровень языка программирования?
В настоящее время в мире существует несколько сотен реально используемых
языков программирования. Для каждого есть своя область применения.
Любой алгоритм, как мы знаем, есть последовательность
предписаний, выполнив которые можно за конечное число шагов перейти от
исходных данных к результату. В зависимости от степени детализации
предписаний обычно определяется уровень языка программирования — чем
меньше детализация, тем выше уровень языка.
По этому критерию можно выделить следующие
уровни языков программирования:
- машинные;
- машинно-оpиентиpованные (ассемблеpы);
- машинно-независимые (языки высокого уровня).
Машинные языки и машинно-ориентированные языки —
это языки низкого уровня, требующие указания мелких
деталей процесса обработки данных. Языки же высокого уровня имитируют
естественные языки, используя некоторые слова разговорного языка и общепринятые математические
символы. Эти языки более удобны для человека.
Языки высокого уровня делятся на:
- процедурные (алгоритмические) (Basic, Pascal, C и др.), которые
предназначены для однозначного описания алгоритмов; для решения задачи процедурные
языки требуют в той или иной форме явно записать процедуру ее решения;
- логические (Prolog, Lisp и др.), которые ориентированы не на
разработку алгоритма решения задачи, а на систематическое и формализованное
описание задачи с тем, чтобы решение следовало из составленного
описания;
- объектно-ориентированные (Object Pascal, C++, Java и др.), в
основе которых лежит понятие объекта, сочетающего в себе данные и действия
над нами. Программа на объектно-ориентированном языке, решая некоторую
задачу, по сути описывает часть мира, относящуюся к этой задаче. Описание
действительности в форме системы взаимодействующих объектов естественнее,
чем в форме взаимодействующих процедур.
7.14. Какие у машинных языков достоинства и недостатки?
Каждый компьютер имеет свой машинный язык,
то есть свою совокупность машинных команд, которая отличается количеством
адресов в команде, назначением информации, задаваемой в адресах, набором
операций, которые может выполнить машина и др.
При программировании на машинном языке программист может держать под своим контролем каждую команду и каждую ячейку
памяти, использовать все возможности имеющихся машинных операций.
Но процесс написания программы на машинном языке очень
трудоемкий и утомительный. Программа получается громоздкой,
труднообозримой, ее трудно отлаживать, изменять и развивать.
Поэтому в случае, когда нужно иметь эффективную программу, в
максимальной степени учитывающую специфику конкретного компьютера,
вместо машинных языков используют близкие к ним машинно-ориентированные
языки (ассемблеры).
7.15. Что такое язык ассемблера?
|
Язык ассемблера — это машинно-зависимый язык низкого уровня, в котором
короткие мнемонические имена соответствуют отдельным машинным командам. Используется для представления в удобочитаемой
форме программ, записанных в машинном коде.
|
Язык ассемблера позволяет программисту пользоваться текстовыми мнемоническими
(то есть легко запоминаемыми человеком) кодами, по своему усмотрению
присваивать символические имена регистрам компьютера и памяти, а также
задавать удобные для себя способы адресации. Кроме того, он позволяет
использовать различные системы счисления (например, десятичную или
шестнадцатеричную) для представления числовых констант, использовать в
программе комментарии и др.
Программы, написанные на языке ассемблера, требуют значительно меньшего
объема памяти и времени выполнения. Знание программистом языка ассемблера
и машинного кода дает ему понимание архитектуры машины. Несмотря на то, что
большинство специалистов в области программного обеспечения разрабатывают
программы на языках высокого уровня, таких, как Object Pascal или C, наиболее
мощное и эффективное программное обеспечение полностью или частично написано
на языке ассемблера.
Языки высокого уровня были разработаны для того, чтобы освободить
программиста от учета технических особенностей конкретных компьютеров,
их архитектуры. В противоположность этому, язык ассемблера разработан с
целью учесть конкретную специфику процессора. Сдедовательно, для того,
чтобы написать программу на языке ассемблера для конкретного компьютера, важно
знать его архитектуру [57].
В качестве примера приведем программу на языке ассемблера для IBM PC.
Программа вычисляет значение a = b + c для целых a, b и c:
.MODEL SMALL
.DATA
b DW 5
c DW 3
a DW ?
.CODE
begin MOV AX,@DATA
MOV DS,AX
MOV AX,B
ADD AX,C
MOV A,AX
MOV AH,4CH
INT 21H
END begin
|
Директива .MODEL задает механизм распределения памяти под данные и команды.
Директива .DATA определяет начало участка программы с данными.
Директивы DW задают типы переменных и их значения.
Директива .CODE определяет начало участка программы с командами.
Команды MOV AX,@DATA и MOV DS,AX
записывают адрес сегмента данных в регистр DS (Data Segment).
Для вычисления a используются команды MOV AX, B,
ADD AX,C и MOV A,AX.
В директиве END задана метка первой выполняемой программы программы begin.
|
Перевод программы с языка ассемблера на машинный язык осуществляется
специальной программой, которая называется ассемблером и является,
по сути, простейшим транслятором.
7.16. В чем преимущества алгоритмических языков перед машинными?
Основные преимущества таковы:
- алфавит алгоритмического языка значительно
шире алфавита машинного языка, что существенно повы шает наглядность
текста программы;
- набор операций, допустимых для использования,
не зависит от набора машинных операций, а выбирается из соображений
удобства формулирования алгоритмов решения задач определенного класса;
- формат предложений достаточно гибок
и удобен для использования, что позволяет с помощью одного пред ложения
задать достаточно содержательный этап обра ботки данных;
- требуемые операции задаются с помощью общепринятых
математических обозначений;
- данным в алгоритмических языках присваиваются
индивидуальные имена, выбираемые программистом;
- в языке может быть предусмотрен значительно
более широкий набор типов данных по сравнению с набором машинных
типов данных.
Таким образом, алгоритмические языки в значительной
мере являются машинно-независимыми. Они облегчают работу программиста
и повышают надежность создаваемых программ.
7.17. Какие компоненты образуют алгоритмический язык?
|
Алгоритмический язык (как и любой другой язык) образуют три его составляющие:
алфавит, синтаксис и семантика.
|
Алфавит —
это фиксированный для данного языка набор основных символов, т.е.
"букв алфавита", из которых должен состоять любой текст на этом языке
— никакие другие символы в тексте не допускаются.
Синтаксис
— это правила построения фраз, позволяющие определить, правильно
или неправильно написана та или иная фраза. Точнее говоря, синтаксис
языка представляет собой набор правил, устанавливающих, какие комбинации
символов являются осмысленными предложениями на этом языке.
Семантика
определяет смысловое значение предложений языка. Являясь системой правил
истолкования отдельных языковых конструкций, семантика устанавливает,
какие последовательности действий описываются теми или иными фразами языка
и, в конечном итоге, какой алгоритм определен данным текстом на
алгоритмическом языке.
7.18. Какие понятия используют алгоритмические языки?
Каждое понятие алгоритмического языка подразумевает
некоторую синтаксическую единицу (конструкцию) и определяемые ею свойства
программных объектов или процесса обработки данных.
|
Понятие языка определяется во
взаимодействии синтаксических и семантических правил. Синтаксические правила
показывают, как образуется данное понятие из других понятий и букв алфавита,
а семантические правила определяют свойства данного понятия
|
Основными понятиями в алгоритмических языках обычно являются следующие.
1. Имена (идентификаторы) — употpебляются для обозначения
объектов пpогpаммы (пеpеменных, массивов, функций и дp.).
2. Опеpации. Типы операций:
- аpифметические опеpации + , — , * , / и дp. ;
- логические опеpации и , или , не ;
- опеpации отношения < , > , <= , >= , = , <> ;
- опеpация сцепки (иначе, "присоединения",
"конкатенации" ) символьных значений дpуг с другом с образованием одной
длинной строки; изображается знаком "+".
3. Данные
— величины, обpабатываемые пpогpаммой. Имеется тpи основных
вида данных: константы, пеpеменные и массивы.
- Константы — это данные, которые зафиксированы
в тексте программы и не изменяются в процессе ее выполнения.
Пpимеpы констант:
- числовые 7.5 , 12 ;
- логические да (истина), нет (ложь);
- символьные (содержат ровно один символ) "А" , "+" ;
- литеpные (содержат произвольное количество символов) "a0", "Мир", "" (пустая строка).
- Пеpеменные обозначаются именами и могут изменять свои
значения в ходе выполнения пpогpаммы. Пеpеменные бывают целые,
вещественные, логические, символьные и литерные.
- Массивы — последовательности однотипных
элементов, число которых фиксировано и которым присвоено одно
имя. Положение элемента в массиве однозначно определяется его
индексами (одним, в случае одномерного массива, или несколькими,
если массив многомерный). Иногда массивы называют таблицами.
4. Выpажения
— пpедназначаются для выполнения необходимых вычислений,
состоят из констант, пеpеменных, указателей функций (напpимеp, exp(x)),
объединенных знаками опеpаций.
Выражения записываются в виде линейных последовательностей
символов (без подстрочных и надстрочных символов, "многоэтажных"
дробей и т.д.), что позволяет вводить их в компьютер, последовательно
нажимая на соответствующие клавиши клавиатуры.
Различают выражения арифметические, логические и строковые.
- Арифметические выражения служат для определения одного числового
значения. Например, (1+sin(x))/2. Значение этого выражения
при x=0 равно 0.5, а при x=p/2 — единице.
- Логические выражения описывают некоторые условия, которые могут
удовлетворяться или не удовлетворяться. Таким образом, логическое
выражение может принимать только два значения — "истина"
или "ложь" (да или нет). Рассмотрим в качестве примера
логическое выражение x*x + y*y < r*r , определяющее принадлежность точки
с координатами (x, y) внутренней области круга радиусом r c центром в начале
координат. При x=1, y=1, r=2 значение этого выражения — "истина",
а при x=2, y=2, r=1 — "ложь".
- Cтроковые (литерные) выражения, значениями которых являются текcты.
В строковые выражения могут входить литерные и строковые константы, литерные
и строковые переменные, литерные функции, разделенные знаками операции сцепки.
Например, А + В означает присоединение строки В к концу строки А .
Если А = "куст ", а В = "зеленый",
то значение выражения А + В есть "куст зеленый".
5. Операторы
(команды). Оператор — это наиболее крупное и содержательное
понятие языка: каждый оператор представляет собой законченную фразу
языка и определяет некоторый вполне законченный этап обработки
данных. В состав опеpатоpов входят:
- ключевые слова;
- данные;
- выpажения и т.д.
Операторы подpазделяются на исполняемые и неисполняемые.
Неисполняемые опеpатоpы пpедназначены для описания данных и
стpуктуpы пpогpаммы, а исполняемые — для выполнения pазличных
действий (напpимеp, опеpатоp пpисваивания, опеpатоpы ввода и вывода,
условный оператор, операторы цикла, оператор процедуры и дp.).
7.19. Что такое стандартная функция?
При решении различных задач с помощью компьютера
бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
|
Вычисления часто употребляемых функций осуществляются посредством
подпрограмм, называемых стандартными функциями, которые заранее
запрограммированы и встроены в транслятор языка.
|
Таблица стандартных функций школьного алгоритмического языка
|
Название и математическое
обозначение функции |
Указатель функции |
| Абсолютная величина (модуль) |
| х | |
abs(x) |
| Корень квадратный | 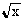 |
sqrt(x) |
| Натуральный логарифм |
ln x |
ln(x) |
| Десятичный логарифм |
lg x |
lg(x) |
| Экспонента (степень числа е ~ 2.72) |
ex |
exp(x) |
| Знак числа x ( - 1, если х<0;
0, если x = 0; 1, если x > 0) |
sign x |
sign(x) |
| Целая часть х (т.е. максимальное
целое число,не превосходящее х) |
|
int(x) |
| Минимум из чисел х и y |
|
min(x,y) |
| Максимум из чисел х и y |
|
max(x,y) |
| Частное от деления целого
х на целое y |
|
div(x,y) |
| Остаток от деления целого
х на целое y |
|
mod(x,y) |
| Случайное число
в диапазоне от 0 до х - 1 |
|
rnd(x) |
| Синус (угол в радианах) |
sin x |
sin(x) |
| Косинус (угол в радианах) |
cos x |
cos(x) |
| Тангенс (угол в радианах) |
tg x |
tg(x) |
| Котангенс (угол в радианах) |
ctg x |
ctg(x) |
| Арксинус (главное значение
в радианах) |
arcsin x |
arcsin(x) |
| Арккосинус (главное значение
в радианах) |
arccos x |
arccos(x) |
| Арктангенс (главное значение
в радианах) |
arctg x |
arctg(x) |
| Арккотангенс
(главное значение в радианах) |
arcctg x |
arcctg(x) |
В качестве аргументов функций можно использовать
константы, переменные и выражения. Например:
sin ( 3.05 )
min ( a, 5) |
sin ( x )
min ( a, b ) |
sin ( 2 * y + t / 2 )
min ( a + b , a * b ) |
sin((exp(x) + 1) ** 2)
min(min(a, b), min(c, d)) |
Каждый язык программирования имеет свой набор стандартных функций.
7.20. Как записываются арифметические выражения?
Арифметические выражения записываются по следующим правилам:
- Нельзя опускать знак умножения между сомножителями
и ставить рядом два знака операций.
- Индексы элементов массивов записываются в
квадратных (школьный АЯ, Pascal) или круглых (Basic) скобках.
- Для обозначения переменных используются буквы латинского алфавита.
- Операции выполняются в порядке старшинства:
сначала вычисление функций, затем возведение в степень, потом умножение
и деление и в последнюю очередь — сложение и вычитание.
- Операции одного старшинства выполняются
слева направо. Однако, в школьном АЯ есть одно исключение из этого правила: операции возведения в
степень выполняются справа налево. Так, выражение 2**(3**2) в школьном
АЯ вычисляется как 2**(3**2) = 512. В языке QBasic аналогичное выражение
2^3^2 вычисляется как (2^3)^2 = 64. А в языке Pascal вообще не
предусмотрена операция возведения в степень, в Pascal x^y записывается
как exp(y*ln(x)), а x^y^z как exp(exp(z*ln(y))*ln(x)).
Примеры записи арифметических выражений
| Математическая запись |
Запись на школьном алгоритмическом языке |
 |
x * y / z |
 |
x / ( y * z ) или x / y / z |
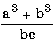 |
( a**3 + b**3 ) / ( b*c ) |
 |
( a[i+1] + b[i-1] ) / ( 2*x*y ) |
 |
( -b + sqrt(b*b - 4*a*c)) / ( 2*a ) |
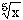 (x<0) (x<0) |
sign(x) * abs(x) ** (1/5) |
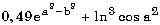 |
0.49 * exp(a*a - b*b) + ln(cos(a*a)) ** 3 |
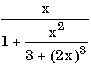 |
x/(1 + x*x/(3 + (2*x)**3)) |
Типичные ошибки в записи выражений:
5x + 1
a + sin x
((a + b)/c**3
|
Пропущен знак умножения между 5 и х
Аргумент x функции sin x не заключен в скобки
Не хватает закрывающей скобки
|
7.21. Как записываются логические выражения?
В записи логических выражений помимо арифметических операций сложения, вычитания, умножения, деления
и возведения в степень используются операции отношения < (меньше),
<= (меньше или равно), > (больше), >= (больше или равно), = (равно),
<> (не равно), а также логические операции и, или, не.
Примеры записи логических выражений, истинных при выполнении
указанных условий.
| Условие |
Запись на школьном алгоритмическом языке |
| Дробная часть вещественого числа a равна нулю |
int(a) = 0 |
| Целое число a — четное |
mod(a, 2) = 0 |
| Целое число a — нечетное |
mod(a, 2) = 1 |
| Целое число k кратно семи |
mod(a, 7) = 0 |
| Каждое из чисел a, b положительно |
(a>0) и (b>0) |
| Только одно из чисел a, b положительно |
((a>0) и (b<=0)) или
((a<=0) и (b>0)) |
| Хотя бы одно из чисел a, b, c является отрицательным |
(a<0) или (b<0) или
(c<0) |
| Число x удовлетворяет условию a < x < b |
(x>a) и (x<b) |
| Число x имеет значение в промежутке [1, 3] |
(x>=1) и (x<=3) |
| Целые числа a и b имеют одинаковую четность |
((mod(a, 2)=0) и (mod(b, 2)=0) или
((mod(a, 2)=1) и (mod(b, 2)=1)) |
| Точка с координатами (x, y) лежит в круге
радиуса r с центром в точке (a, b) |
(x-a)**2 + (y-b)**2 < r*r |
| Уравнение ax^2 + bx + c = 0 не имеет действительных корней |
b*b - 4*a*c < 0 |
| Точка (x, y) принадлежит первой или третьей четверти |
((x>0) и (y>0)) или
((x<0) и (y>0)) |
| Точка (x, y) принадлежит внешности единичного
круга с центром в начале координат или его второй четверти |
(x*x + y*y > 1) или
((x*x + y*y <= 1) и
(x<0) и (y>0)) |
| Целые числа a и b являются взаимнопротивоположными |
a = -b |
| Целые числа a и b являются взаимнообратными |
a*b = 1 |
| Число a больше среднего арифметического чисел b, c, d |
a > (b+c+d) / 3 |
| Число a не меньше среднего геометрического чисел b, c, d |
a >= (b+c+d) ** (1/3) |
| Хотя бы одна из логических переменных F1 и F2 имеет значение да |
F1 или F2 |
| Обе логические переменые F1 и F2 имеют значение да |
F1 и F2 |
| Обе логические переменые F1 и F2 имеют значение нет |
не F1 и не F2 |
| Логическая переменная F1 имеет значение
да, а логическая переменная F2 имеет значение нет |
F1 и не F2 |
| Только одна из логических
переменных F1 и F2 имеет значение да |
(F1 и не F2) или
(F2 и не F1) |
7.22. Упражнения
7.1. Запишите по правилам алгоритмического языка выражения:
| a) |
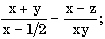 |
e) |
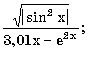 |
| б) |
 |
ж) |
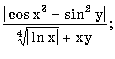 |
| в) |
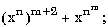 |
з) |
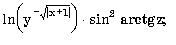 |
| г) |
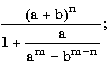 |
и) |
 |
| д) |
 |
к) |
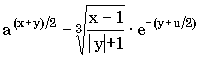 |
[ Ответ ]
7.2. Запишите в обычной математической форме арифметические
выражения:
а) a / b ** 2;
б) a+b/c+1;
в) 1/a*b/c;
г) a**b**c/2;
д) (a**b)**c/2;
е) a/b/c/d*p*q;
ж) x**y**z/a/b;
з) 4/3*3.14*r**3;
и) b/sqrt(a*a+b);
к) d*c/2/R+a**3; |
л) 5*arctg(x)-arctg(y)/4;
м) lg(u*(1/3)+sqrt(v)+z);
н) ln(y*(-sqrt(abs(x))));
о) abs(x**(y/x)-(y/x)**(1/3));
п) sqrt((x1-x2)**2+(y1-y2)**2);
р) exp(abs(x-y))*(tg(z)**2+1)**x;
c) lg(sqrt(exp(x-y))+x**abs(y)+z);
т) sqrt(exp(a*x)*sin(x)**n)/cos(x)**2;
у) sqrt(sin(arctg(u))**2+abs(cos(v)));
ф) abs(cos(x)+cos(y))**(1+sin(y)**2); |
[ Ответ ]
7.3. Вычислите значения арифметических выражений при x=1:
а) abs(x-3)/ln(exp(3))*2/lg(10000);
Решение: abs(1-3)=2; ln(exp(3))=3; lg(10000)=4; 2/3*2/4=0.33;
б) sign(sqrt(sqrt(x+15)))*2**2**2;
в) int(-2.1)*int(-2.9)/int(2.9)+x;
г) -sqrt(x+3)**2**(sign(x+0.5)*3)+tg(0);
д) lg(x)+cos(x**2-1)*sqrt(x+8)-div(2,5);
е) sign(x-2)*sqrt(int(4.3))/abs(min(2,-1));
ж) div(10,x+2)*mod(10,x+6)/max(10,x)*mod(2,5).
[ Ответ ]
7.4. Запишите арифметические выражения, значениями которых являются:
а) площадь треугольника со сторонами a, b, c (a, b, c>0)
и полупериметром p;
Ответ: sqrt(p*(p-a)*(p-b)*(p-c));
б) среднее арифметическое и среднее геометрическое чисел a, b, c,
d;
в) расстояние от точки с координатами (x,y) до точки (0,0);
г) синус от x градусов;
д) площадь поверхности куба (длина ребра равна а);
е) радиус описанной сферы куба (длина ребра равна а);
ж) координаты точки пересечения двух прямых, заданных уравнениями
a1x+b1y+c1=0 и a2x+b2y+c2=0
(прямые не параллельны).
[ Ответ ]
7.5. Вычислите значения логических выражений:
а) x*x+y*y<=9 при x=1, y=-2
Ответ: да;
б) b*b-4*a*c<0 при a=2, b=1, c=-2;
в) (a>=1) и (a<=2) при a=1.5;
г) (a<1) или (a>1.2) при a=1.5;
д) (mod(a,7)=1) и (div(a,7)=1) при a=8;
е) не ((a>b) и (a<9) или (а*а=4)) при
a=5, b=4.
[ Ответ ]
7.6. Запишите логические выражения, истинные только при выполнении указанных
условий:
а) x принадлежит отрезку [a, b]
Ответ: (x>=a) и (x<=b);
б) x лежит вне отрезка [a, b];
в) x принадлежит отрезку [a, b] или отрезку [c, d];
г) x лежит вне отрезков [a, b] и [c, d];
д) целое k является нечетным числом;
е) целое k является трехзначным числом, кратным пяти;
ж) элемент ai,j двумерного массива находится на пересечении
нечетной строки и четного столбца;
з) прямые a1x+b1y+c1=0 и a2x+b2y+c2=0
параллельны;
и) из чисел a, b, c меньшим является с, а большим b;
к) среди чисел a, b, c, d есть взаимно противоположные;
л) среди целых чисел a, b, c есть хотя бы два четных;
м) из отрезков с длинами a, b, c можно построить треугольник;
н) треугольники со сторонами a1, b1, c1
и a2, b2, c2 подобны;
о) точка с координатами (x,y) принадлежит внутренней области треугольника
с вершинами A(0,5), B(5,0) и C(1,0);
п) точка с координатами (x,y) принадлежит области, внешней по
отношению к треугольнику с вершинами A(0,5), B(1,0) и C(5,0);
р) четырехугольник со сторонами a, b, c и d является ромбом.
[ Ответ ]
7.7. Начертите на плоскости (x,y) область, в которой и только
в которой истинно указанное выражение. Границу, не принадлежащую этой области,
изобразите пунктиром.
а) (x<=0) и (y>=0)
Ответ:

|
е) ((x-2)**2+y*y<=4) и (y>x/2)
Ответ:

|
б) (x>=0) или (y<=0)
в) x+y>=0
г) (x+y>0) и (y<0)
д) abs(x)+abs(y)>=1
|
ж) (x*x+y*y<1) и (y>x*x);
з) (y>=x) и (y+x>=0) и (y<=1);
и) (abs(x)<=1) и (y<2);
к) (x**2+y**2<4) и (x**2+y**2>1);
|
[ Ответ ]
7.8. Запишите логическое выражение, которое принимает значение "истина"
тогда и только тогда, когда точка с координатами (x, y) принадлежит заштрихованной
области.
[ Ответ ]
7.9. Пусть a=3, b=5, c=7. Какие значения будут
иметь эти переменные в результате выполнения последовательности операторов:
а) a:=a+1; b:=a+b; c:=a+b; a:=sqrt(a)
Решение: a=3+1=4, b=4+5=9, c=4+9=13,
a= {корень квадратный из} 4 =2.
Ответ: а=2, b=9, c=13;
б) с:=a*b+2; b:=b+1; a:=c-b**2; b:=b*a;
в) b:=b+a; c:=c+b; b:=1/b*c;
г) p:=c; c:=b; b:=a; a:=p; c:=a*b*c*p;
д) c:=a**(b-3); b:=b-3; a:=(c+1)/2*b; c:=(a+b)*a;
е) x:=a; a:=b; b:=c; c:=x; a:=sqrt(a+b+c+x-2);
ж) b:=(a+c)**2; a:=lg(b**2)**2; c:=c*a*b.
[ Ответ ]
7.10. Задайте с помощью операторов присваивания следующие действия:
а) массив X=(x1, x2) преобразовать по правилу:
в качестве x1 взять сумму, а в качестве х2 — произведение
исходных компонент;
Решение: c:=x[1]; x[1]:=x[1]+x[2]; x[2]:=c*x[2]
б) поменять местами значения элементов массива X=(x1, x2);
в) в массиве A(N) компоненту с номером i (1<i<N)
заменить полусуммой исходных соседних с нею компонент, соседнюю справа компоненту
заменить на нуль, а соседнюю слева компоненту увеличить на 0.5;
г) u = max(x, y, z) + min(x-z, y+z, y, z);
[ Ответ ]
7.11. Задайте с помощью команд если или выбор вычисления
по формулам:
| a) |
 |
| б) |
 |
| в) |
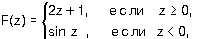
где
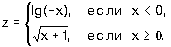 |
| г) |
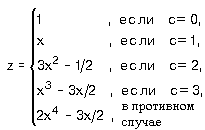 |
| д) |
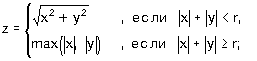 |
| е) |
 |
| ж) |
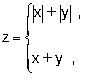 |
если точка лежит внутри круга радиусом r (r>0) с центром в точке (a,b)
в противном случае |
[ Ответ ]
7.12. Постройте графики функций y(x), заданных командами
если:
а) если x<=-1
то y:=1/x**2
иначе
если x<=2
то y:=x*x
иначе y:=4
все
все |
в) если x<-0.5
то y:=1/abs(x)
иначе
если x<1
то y:=2
иначе y:=1/(x-0.5)
все
все |
Решение
 |
г) если x<0
то y:=1
иначе
если x<3.14
то y:=cos(x)
иначе y:=-1
все
все |
б) если x<-5
то y:=-5
иначе
если x<0
то y:=x
иначе
если x<3
то y:=2*x
иначе y:=6
все
все
все |
д) если abs(x)>2
то y:=x*x
иначе
если x<0
то y:=-2*x
иначе
если x>=1
то y:=4
иначе y:=4*x*x
все
все
все |
[ Ответ ]
7.13. Определите значение целочисленной переменной S после выполнения
операторов:
а) S:=128
нц для i от 1 до 4
S:=div(S,2)
кц
|
Решение
| i |
S |
| |
128 |
| 1 |
128/2=64 |
| 2 |
64/2=32 |
| 3 |
32/2=16 |
| 4 |
16/2=8 |
Ответ: S=8 |
г) S:=0
нц для i от 1 до 2
нц для j от 2 до 3
S:=S+i+j
кц
кц |
Решение
| i |
j |
S |
| |
|
0 |
| 1 |
2 |
0+1+2=3 |
| |
3 |
3+1+3=7 |
| 2 |
2 |
7+2+2=11 |
| |
3 |
11+2+3=16 |
Ответ: S=16 |
б) S:=1; a:=1
нц для i от 1 до 3
S:=S+i*(i+1)*a
a:=a+2
кц |
д) нц для i от 1 до 3
S:=0
нц для j от 2 до 3
S:=S+i+j
кц
кц |
в) S:=1; a:=1
нц для i от 1 до 3
S := S+i
нц для j oт 2 до 3
S := S+j
кц
кц |
е) нц для i от 1 до 2
S := 0
нц для j oт 2 до 3
нц для k oт 1 до 2
S := S+i+j+k
кц
кц
кц |
[ Ответ ]
7.14. Определите значение переменной S после выполнения операторов:
а) i:=0; S:=0
нц пока i<3
i:=i+1;
S:=S+i*i
кц |
г) S:=0; N:=125
нц пока N>0
S:=S+mod(N,10) | S — сумма цифр
N:=div(N,10) | числа N
кц |
Решение
| Условие i < 3 |
i |
S |
| |
0 |
0 |
| 0 < 3? да |
1 |
0+12=1 |
| 1 < 3? да |
2 |
1+22=5 |
| 2 < 3? да |
3 |
5+32=14 |
| 3 < 3? нет(кц) |
|
|
Ответ: S=14 |
Решение
| Условие N > 0 |
S |
N |
| |
0 |
125 |
| 125 > 0? да |
0+5=5 |
12 |
| 12 > 0? да |
5+2=7 |
1 |
| 1 > 0? да |
7+1=8 |
0 |
| 0 > 0? нет (кц) |
|
|
Ответ: S=8 |
б) S:=0; i:=1
нц пока i>1
S:=S+1/i
i:=i-1
кц |
д) а:=1; b:=1; S:=0;
нц пока a<=5
a:=a+b; b:=b+a;
S:=S+a+b
кц |
в) S:=0; i:=1; j:=5
нц пока i<j
S:=S+i*j
i:=i+1
j:=j-1
кц |
е) a:=1; b:=1
нц пока a+b<10
a:=a+1
b:=b+a
кц
S:=a+b |
[ Ответ ]
7.15. Составьте алгоритмы решения задач линейной структуры
(условия этих задач заимствованы из учебного пособия В.М. Заварыкина,
В.Г. Житомирского и М.П. Лапчика "Основы информатики и вычислительной
техники", 1989):
а) в треугольнике известны три стороны a, b и c;
найти (в градусах) углы этого треугольника, используя формулы:
 |
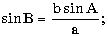 |
С=180o-(А+В). |
Пояснение. Обратите внимание на то, что стандартные тригонометрические
функции arccos и arcsin возвращают вычисленное значение
в радианной мере.
Решение:
алг Углы треугольника(арг вещ a,b,c, рез вещ UgolA,UgolB,UgolC)
нач вещ RadGr,UgolARad
| RadGr — коэф. перевода угла из радианной меры в градусную
| UgolARad — угол A (в радианах)
RadGr:=180/3.14
UgolARad:=ArcCos((b*b+c*c-a*a)/(2*b*c))
UgolA:=UgolARad*RadGr
UgolB:=ArcSin(b*sin(UgolARad)/a)*RadGr
UgolC:=180-(UgolA+UgolB)
кон
б) в треугольнике известны две стороны a, b и угол C
(в радианах) между ними; найти сторону c, углы A и B
(в радианах) и площадь треугольника, используя формулы:
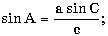
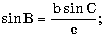
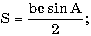 с2 = a2 + b2 - 2ab cos C.
Пояснение. Сначала нужно найти сторону c , а затем остальные
требуемые значения;
с2 = a2 + b2 - 2ab cos C.
Пояснение. Сначала нужно найти сторону c , а затем остальные
требуемые значения;
в) в треугольнике известны три стороны a, b и c;
найти радиус описанной окружности и угол A (в градусах), используя
формулы:
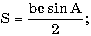
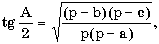 где
где 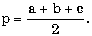
г) в правильной треугольной пирамиде известны
сторона основания a и угол A (в градусах) наклона боковой
грани к плоскости основания; найти объем и площадь полной поверхности
пирамиды, используя формулы:
д) в усеченном конусе известны радиусы оснований R и r
и угол A (в радианах) наклона образующей к поверхности большего
основания; найти объем и площадь боковой поверхности конуса, используя формулы:
e) в правильной четырехугольной пирамиде сторона основания равна
a , а боковое ребро наклонено к плоскости основания
под углом A ; найти объем и площадь полной поверхности пирамиды и
площадь сечения, проходящего через вершину пирамиды и диагональ основания
d ; использовать формулы:
[ Ответ ]
7.16. Составьте алгоритм решения задач развлетвляющейся структуры:
а) определить, является ли треугольник с заданными сторонами
a, b, c равнобедренным;
Решение:
алг Треугольник(арг вещ a,b,c, рез лог Otvet)
дано | a>0, b>0, c>0, a+b>c, a+c>b, b+c>a
надо | Otvet = да, если треугольник равнобедренный
| Otvet = нет, если треугольник не равноведренный
нач
если (a=b) или (a=c) или (b=c)
то Otvet:= да
иначе Otvet:= нет
все
кон
б) определить количество положительных чисел среди заданных
чисел a, b и c;
в) меньшее из двух заданных неравных чисел увеличить вдвое,
а большее оставить без изменения;
г) числа a и b — катеты одного прямоугольного
треугольника, а c и d — другого; определить, являются ли
эти треугольники подобными;
д) даны три точки на плоскости; определить, какая из них ближе к началу координат;
е) определить, принадлежит ли заданная точка (x, y) плоской
фигуре, являющейся кольцом с центром в начале координат, с внутренним
радиусом r1 и внешним радиусом r2 ;
ж) упорядочить по возрастанию последовательность трех чисел
a, b и c.
[ Ответ ]